Surface Area of Cone
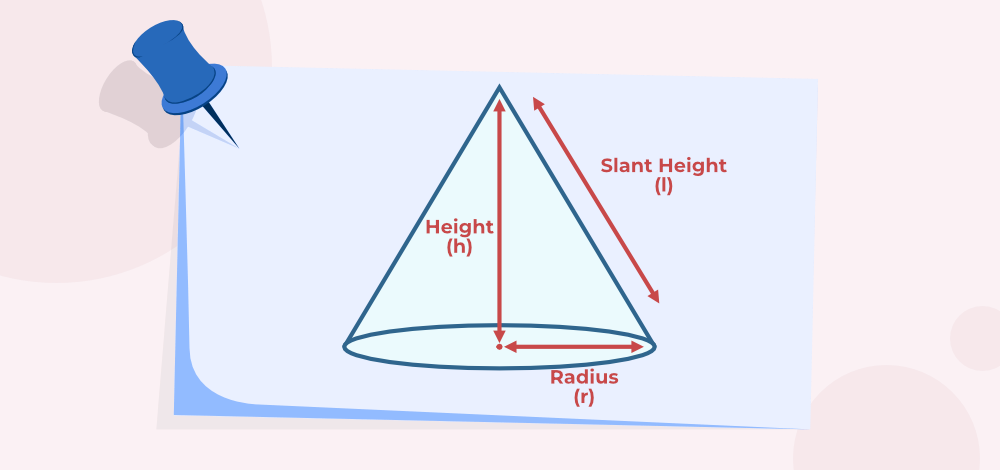
Surface Area of Cone is the total area occupied by the surfaces of the cone. A cone is a three-dimensional-shaped geometric figure that has a flat face and a curved surface with a pointed end. The shape of a cone is obtained by rotating the right-angled triangle about its perpendicular. The pointed end of the cone is called an apex or a vertex. The perpendicular distance between the center of the base and the apex of a cone is called the height, while the slant height is the distance from the apex of the cone to any point on the circumference of the base. A normal cone is also called a right circular cone. The area of a right circular cone is discussed in this article. Ice cream cones, traffic cones, funnels, birthday hats, etc. are some examples of cones that we see in our daily life.

What is the Surface Area of a Cone?
Surface Area of a cone is visualized as the area occupied by the cone when it is cut open. It is formed by a circular base and a curved surface. The surface area of the cone is dependent on the radius of its base and the height of the cone. Also, the volume of a cone depends on its radius and height.
Surface Area of a Cone Formula
The surface area of a cone is defined as the area occupied by the boundary or the surface of a cone. A cone has two kinds of surface areas namely, a curved surface area and a total surface area.
Curved Surface Area of Cone
The Curved surface of a cone is defined as the area of the curved part of the cone, i.e., the area of the cone excluding its base. It is also known as the Lateral Surface area of the cone. Forumla for the CSA (Curved Surface Area) of the cone is given as follows:
where,
“r” is the radius of the base of a cone and
“l” is the slant height of the cone.
Total Surface Area of Cone
The total surface area of a cone is defined as the total area occupied by a cone in a three-dimensional space, i.e., the area of the curved surface and the area of the circular base. Formula for the TSA (Total Surface Area) of the cone is given as follows:
where,
“r” is the radius of the base of a cone and
“l” is the slant height of the cone.
Derivation of Surface Area of a Cone
To observe the figure formed by the surface of a cone, take a paper cone and then cut it along its slant height. Now, mark A and B as the two endpoints and O as the point of the intersection of the two lines. Now if we open this, it will look like a sector of a circle.

So, to find the curved surface area of the cone, we have to find the area of the sector.
The area of the sector in terms of length of arc = (arc length × radius)/ 2 = ((2πr) × l)/2 = πrl.
CSA of a Cone = πrl square units
The total surface area of a cone (T) = Area of the base + Curved Surface area
Since the base is a circle, the area of the base = πr2
⇒ T = πr2 + πrl = πr(r + l)
TSA of the Cone = πr (r + l) square units
Also, learn about the frustum of a cone here.
Relation Between the Surface Area of a Cone and Its Height
Considering the slant height, height, and radius of the cone, they form a right-angle triangle, where slant height is the hypotenuse, the base is the radius of the base and height is the altitude of the right-angle triangle.

Using the Pythagoras Theorem, we get l2 = r2+h2
Thus, the slant height of a cone (l) = √(r2 + h2)
So, by replacing the value of slant in the surface areas formulae of a cone, we get
Curved surface area (S) = πr√(r2 + h2) square units
Total surface area (T) = πr2 + πr√(r2 + h2) square units
How to Find the Surface Area of a Cone?
Let’s consider an example to see how to find the surface area of a cone using its formula.
Example: Find the total surface area of a cone if its radius is 5 inches and its slant height is 12 inches. (Use π = 3.14)
Step 1: Note down the dimensions of the given cone. Here, the slant height of a cone is 12 inches and its radius is 5 inches.
Step 2: We know that the total surface area of the cone = πr (r + l). So, substitute the value of given dimensions in the equation = (3.14) × 5 × (5 + 12) = 266.9 sq. in.
Step 3: Hence, the total surface area of a cone is 266.9 square inches.
Solved Examples on the Surface Area of Cone
Example 1: Find the total surface area of a cone if its radius is 15 cm and its slant height is 10 cm. (Use π = 3.14)
Solution:
Given data,
The radius of cone (r) = 15 cm
The slant height (l) = 10 cm
We know that,
The total surface area of the cone = πr (r + l) square units
= (3.14) × 15 × (15 + 10)
= 1,177.5 sq. cm
Hence, the total surface area of the cone is 1,177.5 sq. cm.
Example 2: What is the height of a cone if its radius is 14 units and its curved surface area is 1100 square units? (Use π = 22/7)
Solution:
Given data,
The radius of cone (r) = 14 units
The curved surface area of the cone = 1100 square units
Let the slant height of the cone be “l” and the height of the cone be “h”.
We know that,
The curved surface area of the cone = πrl square units
⇒ 1100 = (22/7) × 14 × l
⇒ 44 × l = 1100
⇒ l = 1100/44 = 25 units
We know that,
slant height (l) = √(h2 + r2)
⇒ h = √(l2 – r2)
= √(252 – 142) = √429 = 20.71 units
Thus, the height of the cone is 20.71 units.
Example 3: Determine the slant height of the cone if the total surface area of the cone is 525 sq. cm and the radius is 7 cm. (Use π = 22/7)
Solution:
Given data,
The radius of cone (r) = 7 cm
The total surface area of the cone = 525 sq. cm
et the slant height of the cone be “l”.
We know that,
The total surface area of the cone = πr (r + l) square units
⇒ (22/7) × 7 × (7 + l) = 525
⇒ 22 × (7 + l) = 525
⇒ 7 + l = 25
⇒ l = 18 cm
Therefore, the slant height of the cone is 18 cm.
Example 4: Calculate the lateral surface area of a cone whose radius is 24 inches and height is 7 inches. (Use π = 3.14)
Solution:
Given data,
The radius of cone (r) = 24 inches
The height of the cone (h) = 7 inches.
We know that,
slant height (l) = √(h2 + r2)
l = √(72 + 242) = √(625) = 25 inches
We know that,
The curved surface area of the cone = πrl square units
= 3.14 × 24 × 25
= 1884 sq. in
Hence, the curved surface area of the cone is 1884 sq. in.
FAQs on Surface Area of Cone
Question 1: What happens to the curved surface area of a cone when its height is doubled?
Answer:
Curved Surface area of the cone directly depends on the radius of its base.
Curved surface area = πrl
If the radius of cone is doubled its curved surface area also gets doubled.
CSA = π(2r)(l)
= 2πrl
= 2 × original curved surface area
Question 2: How do you find the surface area of the cone?
Answer:
Surface area of con can be calculated in two ways,
CSA = πrl
TSA = πrl(r+l)
where,
r is radius of cone
l is slant height of cone
Question 3: Write the ways to calculate the slant height of a cone.
Answer:
Slant height of a cone is defined by the formula
l=√(r2 + h2) units,
where “r” is the radius and “h” is the height of a cone.
Question 4: Write the formula for the base surface of a Cone.
Answer:
Surface of the base of a Cone is circular and the formula for the base of surface of the cone is πr2 square units.
Question 5: What do we mean by the Surface Area of a Cone?
Answer:
Surface Area of a Cone is the region occupied by the Surface of a Cone in 3-D space. It can be calculated by finding the sum of the lateral area and the base area of the cone.